Posted by marcoc on 29 Giugno 2015 under Matematica, Matematica e Python | 
Cosa s’intende per Metateoria? Che cos’è il teorema dei quattro colori? Cosa c’entrano con Gödel?
Cliccate qui per leggere questo mio articolo e fatemi sapere…..
Potete scaricare qui il programma che ho creato nella versione Python e confrontare la sua potenza di calcolo rispetto alla versione in Pascal e Java…..un altro mondo? (Vi ricordo che in linux basta digitare da terminale python sistform.py e premere invio per far girare il programma)
Cliccare qui per scaricare l’algoritmo nelle tre versioni.
Versione corretta Python …..spero
Posted by marcoc on 23 Dicembre 2014 under Matematica, Matematica e Python |
Ciao ragazzi della III As! Vi ricordate della lezione fatta piegando la carta per rappresentare tutte le coniche irriducibili e poi usando GeoGebra? Di seguito c’è il mio articolo che è stato pubblicato nel 2000 su queste cose. L’unico compito che vi do per le vacanze consiste nel tracciare con la carta, poi anche con GeoGebra, una parabola, un’ellisse ed un’iperbole, seguendo le indicazioni dell’articolo. Le istruzioni per la realizzazione al computer erano per il software Cabrì, ma vanno bene, allo stesso modo, per GeoGebra. Di Giacomi non deve fare il lavoro sulla parabola, perché è l’unico ad averlo già fatto quando era dovuto. A lavoro ultimato mi spedite immagini della carta piegata e dei file di GeoGebra? Buone vacanze!
Clicca qui per visualizzare l’articolo.
Posted by marcoc on 19 Agosto 2014 under Matematica, Matematica e Python |
Salve ragazzi, spero che abbiate letto l’articolo precedente. Se non l’avete fatto, fatelo. Comunque, riassumendo: come un’equazione di primo grado, in due variabili (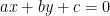
), ha come rappresentazione grafica una retta (i punti della retta sono le soluzioni dell’equazione), così un’equazione di secondo grado in due variabili(
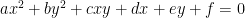) ha (quando possibile) come rappresentazione grafica, nel piano cartesiano, una conica (ellisse, parabola, iperbole o due rette). Dato che nessuno me l’ha spedito, ho pensato di creare io il programma in Python, richiesto nell’articolo precedente. Il vostro compito è quello di provarlo e vedere se non ci sono intoppi. Notate differenze tra questo listato e quello in Pascal? I linguaggi di programmazione come sono cambiati?
La versione di Python è 2.7.6 e la libreria utilizzata per la grafica è Matplotlib scaricabile qui.
Per scaricare il programma clicca …qui
Posted by marcoc on 4 Agosto 2014 under Matematica, Matematica e Python |
Questo articolo è frutto di un lavoro fatto per il prof. Giuseppe Accascina, nel 1991; allora, il software di manipolaziomne simbolica Derive, rappresentava graficamente solo funzioni, cioè curve con espressione y= f(x), oppure in forma parametrica, cioè 
.
Cioè, per rappresentare l’ellisse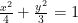 
, era necessario ridurla alla forma 
e poi rappresentare le due funzioni. L’obiettivo che ci eravamo posti era inserire in INPUT i coefficienti a,b,c,d,e,f di un’equazione di II grado, in due variabili (una conica con espressione 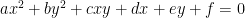) e, ove possibile, tracciarla graficamente nel piano. Si sa che questa equazione può essere costituita da: due rette (conica degenere), una conica a punti immaginari (cioè non rappresentabile nel piano) oppure una parabola o un’ellisse o un’iperbole. Adesso, la cosa fa ridere, perché la rappresentazione grafica di questa equazione è un’operazione che fa tranquillamente anche Geogebra; ma allora non era così scontata la cosa! Dallo studio ne è emerso il programma in Pascal sulle coniche.
Quello che vi chiedo è:
leggere con attenzione l’articolo, senza trascurare le note;
far girare il programma (ho usatoTurbo Pascal, ma dovrebbe andar bene Free Pascal, clicca per scaricare dal sito ufficiale) e provarlo;
implementare il programma in Python, per la grafica vi suggerisco la libreria MATPLOTLIB;
Chiunque, anche non mio alunno, avesse domande o volesse mandarmi il programma in Python può farlo cliccando qui .
Per visualizzare il mio articolo clicca qui.
Per scaricare il programma clicca qui
Posted by marcoc on 28 Luglio 2014 under Matematica, Matematica e Python |
Salve ragazzi! Oggi vi propongo un articolo uscito nel 1997. Dopo aver pubblicato un altro articolo nel 1996 con D’Amore, sono passato ad un’altra rivista di didattica, quella di Mauro Laeng dell’Università di Roma. A Giuseppe Luciano, caporedattore, ho proposto il frutto di piacevoli conversazioni fatte con il professor Giuseppe Frappa, docente di Greco allo ‘J. Stellini’ di Udine e profondo conoscitore della programmazione in Pascal. A lui ho sottoposto l’idea che avevo pensato e da lui ho ricevuto i consigli per realizzarla bene. Di questo articolo vi suggerisco di non perdere le note, sono importanti. L’articolo consiste in un esempio di come il computer si può autoistruire; lo spunto è preso da Gardner nei suoi ‘Enigmi e Giochi matematici’. Ho pensato di allegare anche i programmi da scaricare in un file zip. Oltre che in Pascal, ho implementato il programma in Python, programma in cui ho operato delle variazioni; il file da costruire non è di dati come in Pascal, ma un file di testo.In pratica, il primo programma si può bypassare, scrivendo un file di testo come quello di tuttemoss.text allegato. Cosa vi chiedo?
Ai più svogliati: leggere l’articolo e far girare i programmi in Pascal per vedere se tutto funziona
Ai curiosi: leggere l’articolo e far girare i programmi in Pascal, per vedere se tutto funziona, far girare il programma in Python e vedere se funziona.
Agli esperti: leggere l’articolo e far girare i programmi in Pascal, per vedere se tutto funziona, far girare il programma in Python e vedere se funziona, implementare il programma integrandolo con una buona veste grafica.
Cliccare qui per leggere l’articolo.
Aspetto i vostri contributi e commenti in mail, buon divertimento. Ops! Ho dimenticato di dirvi la versione di Python: 2.7.6 con Ubuntu. Grazie a Valerio Giacomini per le puntualizzazioni e correzioni.
Per scaricare il file zip dei programmi clicca … qui
Posted by marcoc on 14 Luglio 2014 under Matematica, Matematica e Python |
Salve ragazzi! In questa mite estate vi suggerisco una lettura, che ho trovato mettendo a posto gli scaffali della libreria. E’ il mio primo articolo, uscito quando voi non eravate ancora nati ed io avevo appena finito il servizio civile. Dovetti superare l’esame di due referee per poterlo far pubblicare nella rivista di Bruno D’Amore. Suggerisco, a chi non ne sa di programmazione e di funzioni, di leggere le note, che sono la cosa più importante. Chiedo una vostra opinione, se non sul blog per mail. Che cosa ne pensate?
Clicca qui per visualizzare
Di seguito ho pensato, per i più curiosi di poter farvi scaricare il programma; il primo è in pascal e considera l’equazione sin(x)=0 (ovviamente la funzione si può cambiare) senza la derivata (cos(x)); nel secondo si considera la funzione e la sua derivata (il programma dell’articolo). E il terzo? Sorpresa! E’ in Python: il linguaggio del momento. Provate a vedere se funziona!
La versione di Python su cui gira il programma è 2.7.6 per Ubuntu
Per scaricare il file .zip dei programmi clicca……. qui
